//
Qui sotto un'immagine che riassume quanto detto nel podcast QRM.

Puoi anche scaricarla in pdf,
cliccando qui.
Bibliografia
- The Bhagavad Gita. Edizione del 2003. Penguin.
- Giuseppe Tucci (2012). Storia della filosofia indiana. Editori Laterza.
- Sarvepalli Radhakrishnan (2009). Indian Philosophy. Oxford University Press.
//
Qui sotto un'immagine che riassume quanto detto nel podcast QRM.

Puoi anche scaricarla in pdf,
cliccando qui.
Bibliografia
- Steven Pinker (2013). Il declino della violenza. Perché quella che stiamo vivendo è probabilmente l'epoca più pacifica della storia. Mondadori.
- Bear Braumoeller (2019). Only the dead: the persistence of war in the modern age. Oxford University Press.
- Asle Toje, Bård Nikolas Vik Steen (2019). The causes of peace: what we know now. Nobel Symposium Proceedings, Oslo. (In questa collettanea trovate anche un capitolo scritto da Taleb e il sottoscritto).
//
Qui sotto un'immagine che riassume quanto detto nel podcast QRM.
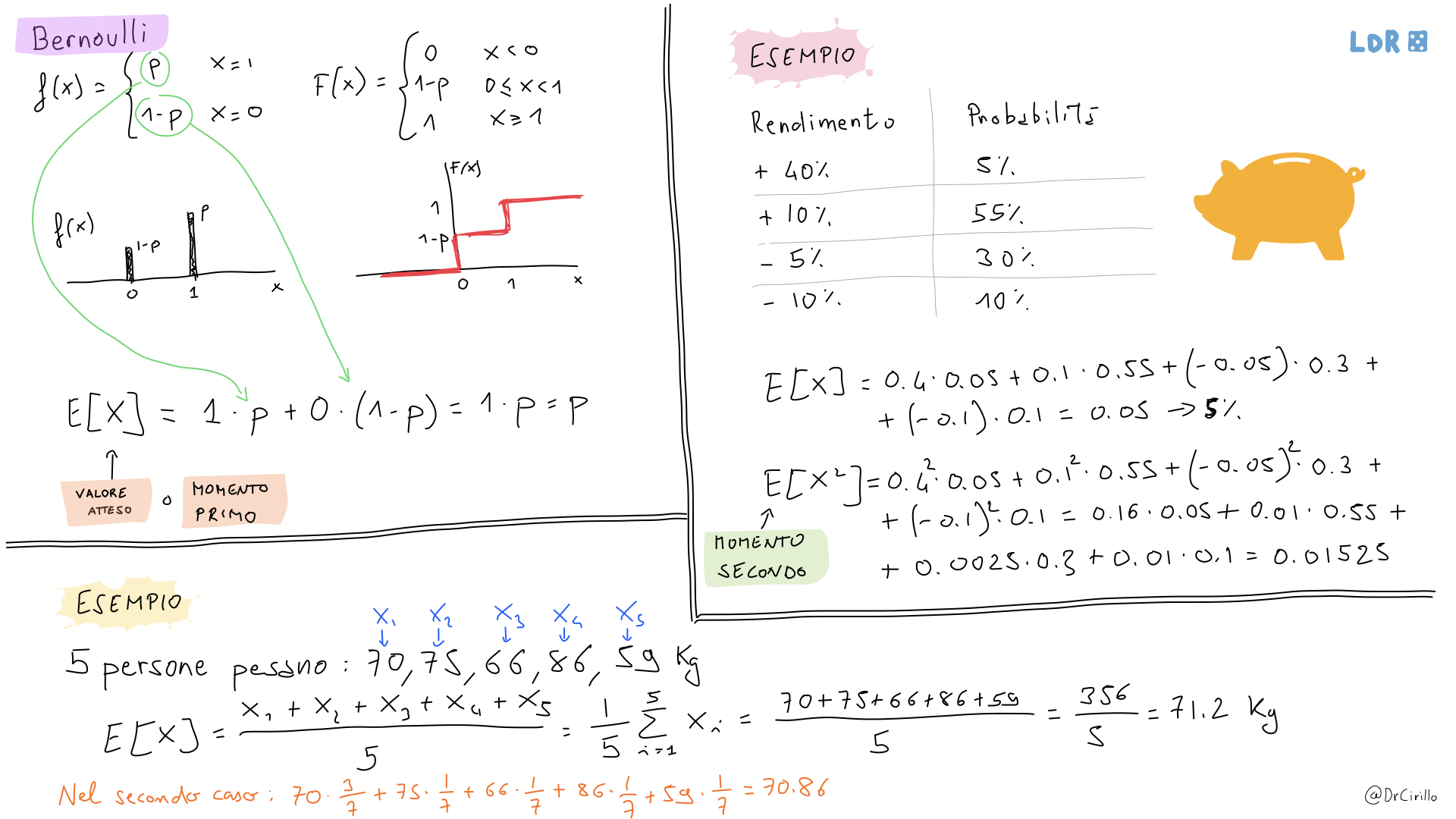
Puoi anche scaricarla in pdf,
cliccando qui.
Bibliografia
- Carl B. Boyer (2017). Storia della matematica. Mondadori.
- Vincenzo di Benedetto (1986). Il medico e la malattia. La scienza di Ippocrate. Einaudi.
//
Qui sotto un'immagine che riassume quanto detto nel podcast.
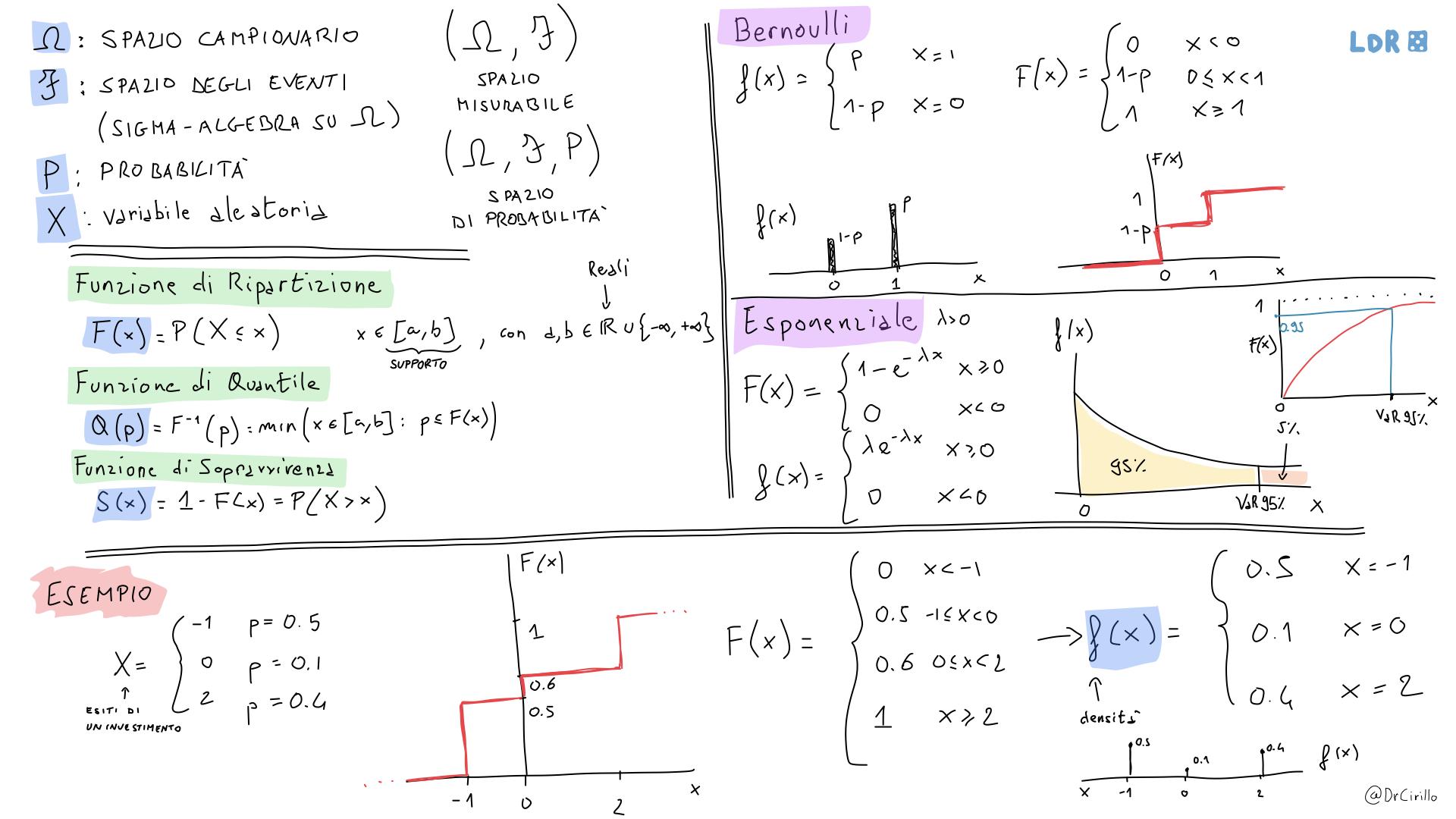
Puoi anche scaricarla in pdf,
cliccando qui.
Bibliografia
- Daniel Kahneman, Olivier Sibony, Cass R. Sunstein (2021). Rumore. Un difetto del ragionamento umano. UTET.
//
Qui sotto un'immagine che riassume quanto detto nel podcast.

Puoi anche scaricarla in pdf,
cliccando qui.
Bibliografia
- Huff Darrel (2007). Mentire con le statistiche. Monti e Ambrosini Editori.
//
Questa è la successione dei risultati dal lancio del nostro dado:
3,
2,
6,
6,
1,
4,
5,
5,
3, …,
n.
A ogni lancio, la frequenza relativa di 5 si aggiorna e può variare.
Se
n è abbastanza grande, convergerà verso il valore limite che cerchiamo.
Bibliografia
- François Walter (2009). Catastrofi, una storia culturale. Colla Editore.
- Donald A. Gillies (1973). An Objective Theory of Probability. Routledge.
- Richard von Mises (1981). Probability, Statistics, and Truth. Dover.









